好一个树形DP。
传送门
题解
他出题人要是敢去掉一条边,我就敢做!!!
首先对于每一个骑士,向他最痛恨的人建一条边。
如果只有$n-1$条边的话,就是一个裸的带权的树上最大独立集。
但是由于要$n$条边,所以最后建出来的应该是一个基环内向树森林。
比如这样:
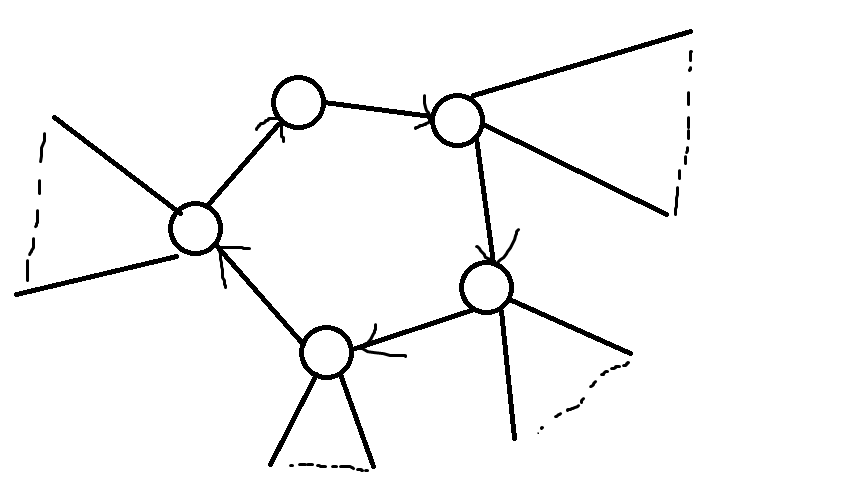
对于在环上的每一个点,可以直接DP出该点选与不选时它与它的子树的最大权值和。
对于环,我们可以再来一趟DP,定义$G[i][0/1/2/3]$:
$G[i][0]$环上第一个点可以选,第$i$个点选时的最大权值和。
$G[i][1]$环上第一个点可以选,第$i$个点不选时的最大权值和。
$G[i][2]$环上第一个点不可以选,第$i$个点选时的最大权值和。
$G[i][3]$环上第一个点不可以选,第$i$个点不选时的最大权值和。
最后的答案为$max(G[n][0],G[n][2],G[n][3])$。
对于每一个环,分别DP,然后把答案加在一起即可。
复杂度:$\Theta(n)$。
代码
1 |
|