「网络流24题」餐巾计划问题

发表于 | 分类于 | | 浏览量： 次

又是一道有意思的网络流。

传送门

洛谷P1251

LOJ6008

数据输入格式略有不同

题解

此题重点在于建模。

首先很显然这题是一个费用流。

但是建模不是很好搞，需要绕几个弯。

首先拆点，将每一天分为早上和下午，早上需要准备好$r_i​$块干净的餐巾，晚上又免费获得了$r_i​$块脏的餐巾。

于是乎可以这样建图：

1.png

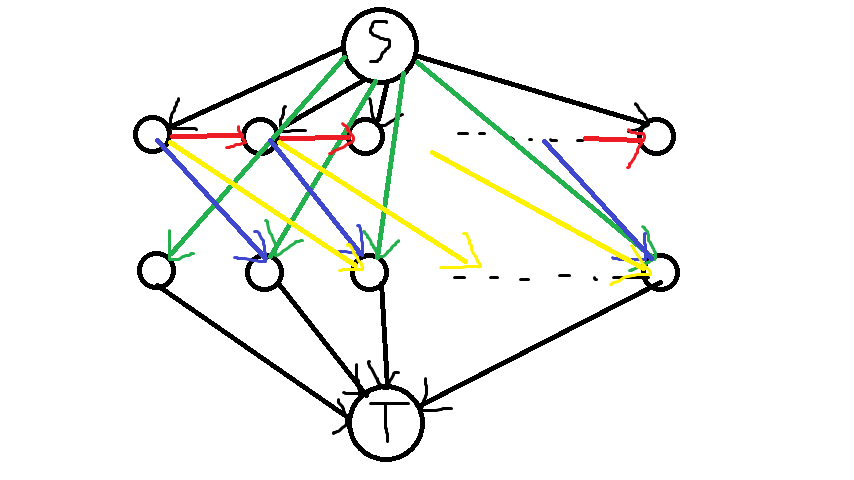
  • 从源点连出$n$条边（绿的那些）到早上（下面那一排点），容量为$+\infty$，代价为$p$。如果需要买新的餐巾，从这些边流过来。

  • 表示早上的$n$个点再连出来$n$条边到汇，容量为$r_i$，代价为$0$。正常情况下这些变必须满载。表示每天早上都可以提供$r_i$条干净的餐巾。

  • 从源点再连出来$n$条边到每一个表示晚上的节点（上面一排），容量为$r_i$，代价为$0$。表示每天晚上可以免费获得$r_i$条脏餐巾。这些边不一定满载，因为脏的餐巾可以扔掉。

  • 表示每一天晚上的节点再连出来一条边到下一天晚上（红的边），容量为$+\infty​$，代价为$0​$。当天的脏餐巾可以放到下一天再处理。

  • 表示每一天晚上的节点连出一条边到$m$天后的早上（蓝的边），容量为$+ \infty$，代价为$f$。表示送去快洗部。
  • 送去慢洗部的同上。

然后直接刷最小费用最大流即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int maxn=4005,maxe=24005,inf=0x3F3F3F3F;
int N,r[2005],p,m,f,n,s,tot,S,T,lnk[maxn],son[maxe],nxt[maxe],w[maxe],cap[maxe],que[maxn],dist[maxn],lst[maxn],pre[maxn],flow[maxn];bool vis[maxn];LL ans;
inline int read()
{
	int ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();}
	return ret*f;
}
inline void add_e(int x,int y,int z,int c)
{
	tot++;son[tot]=y;w[tot]=z;cap[tot]=c;nxt[tot]=lnk[x];lnk[x]=tot;
	tot++;son[tot]=x;w[tot]=-z;cap[tot]=0;nxt[tot]=lnk[y];lnk[y]=tot;
}
inline void MinCostMaxFlow()
{
	while(true)
	{
		memset(dist,63,sizeof(dist));
		memset(flow,63,sizeof(flow));
		int hed=0,til=1;
		que[1]=S;dist[S]=0;vis[S]=true;pre[T]=0;
		while(hed!=til)
		{
			hed=(hed+1)%maxn;vis[que[hed]]=false;
			for(int i=lnk[que[hed]];i;i=nxt[i])
			{
				if(cap[i]>0&&dist[que[hed]]+w[i]<dist[son[i]])
				{
					dist[son[i]]=dist[que[hed]]+w[i];
					lst[son[i]]=i;
					pre[son[i]]=que[hed];
					flow[son[i]]=min(flow[que[hed]],cap[i]);
					if(!vis[son[i]])
					{
						vis[son[i]]=true;
						til=(til+1)%maxn;
						que[til]=son[i];
					}
				}
			}
		}
		if(pre[T]==0) return;
		ans+=(LL)dist[T]*flow[T];
		int p=T;
		while(p!=S)
		{
			cap[lst[p]]-=flow[T];
			cap[(lst[p]&1)?lst[p]+1:lst[p]-1]+=flow[T];
			p=pre[p];
		}
	}
}
int main()
{
	N=read();S=2*N+1;T=2*N+2;
	for(int i=1;i<=N;i++) r[i]=read();
	p=read();m=read();f=read();n=read();s=read();
	for(int i=1;i<=N;i++) add_e(S,i,p,inf);
	for(int i=1;i<=N;i++) add_e(i,T,0,r[i]);
	for(int i=1;i<=N;i++) add_e(S,i+N,0,r[i]);
	for(int i=1;i<N;i++) add_e(i+N,i+N+1,0,inf);
	for(int i=1;i<=N;i++)
	{
		int to1=i+m,to2=i+n;
		if(to1<=N) add_e(i+N,to1,f,inf);
		if(to2<=N) add_e(i+N,to2,s,inf);
	}
	MinCostMaxFlow();
	printf("%lld\n",ans);
	return 0;
}