「网络流24题」运输问题

发表于 | 分类于 | | 浏览量： 次

好经典的模型。

传送门

洛谷P4015

LOJ6011

题解

乍一看就是一个二分图。

但是要求很明显要求最小费用最大流。

考虑如何建模。

由于每一个仓库只能流出定量的货物，但是又不能把每一个仓库看做源。

所以把所有货物都连到同一个源上，连到第$i​$个仓库的边嘚的容量为$A_i​$，费用为$0​$。

每一家零售店又都连到一个汇上，从第$i$家零售店连出的边的容量为$B_i$，费用为$0$。

中间从仓库到零售店的边就按照题目里的说的那样连，容量为$+\infty$。

1.png

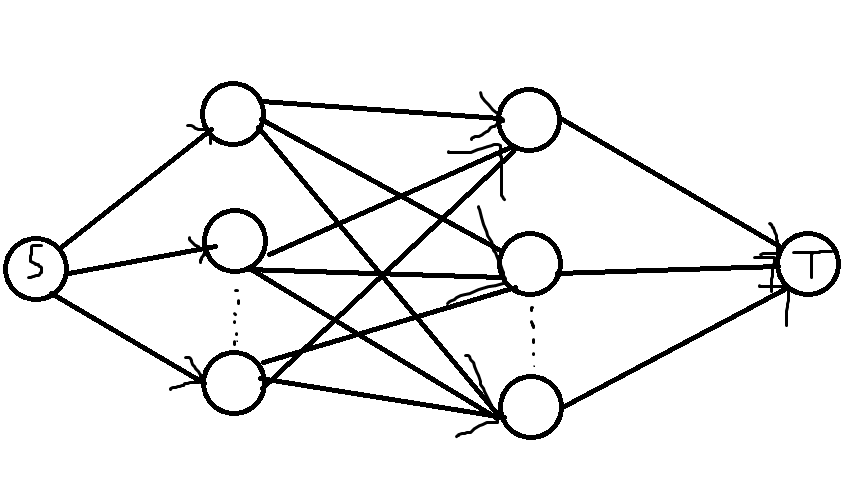
然后直接跑最小费用最大流就好了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=210,maxm=20205,inf=0x3F3F3F3F;
int m,n,S,T,tot,lnk[maxn],son[maxm],nxt[maxm],w[maxm],cap[maxm],que[maxn],lst[maxn],pre[maxn],dist[maxn],flow[maxn],ans;bool vis[maxn];
inline int read()
{
	int ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();}
	return ret*f;
}
inline void add_e(int x,int y,int z,int c){tot++;son[tot]=y;w[tot]=z;cap[tot]=c;nxt[tot]=lnk[x];lnk[x]=tot;}
inline void MinCostMaxFlow(int flg)
{
	while(true)
	{
		if(flg==1) memset(dist,63,sizeof(dist));
		else memset(dist,192,sizeof(dist));
		memset(flow,63,sizeof(flow));
		int hed=0,til=1;
		que[1]=S;dist[S]=0;vis[S]=true;pre[T]=0;
		while(hed!=til)
		{
			hed=(hed+1)%maxn;vis[que[hed]]=false;
			for(int i=lnk[que[hed]];i;i=nxt[i])
			{
				if(cap[i]&&((flg==1&&dist[que[hed]]+w[i]<dist[son[i]])||(flg==-1&&dist[que[hed]]+w[i]>dist[son[i]])))
				{
					dist[son[i]]=dist[que[hed]]+w[i];
					pre[son[i]]=que[hed];
					lst[son[i]]=i;
					flow[son[i]]=min(flow[que[hed]],cap[i]);
					if(!vis[son[i]])
					{
						vis[son[i]]=true;
						til=(til+1)%maxn;
						que[til]=son[i];
					}
				}
			}
		}
		if(pre[T]==0) return;
		ans+=flow[T]*dist[T];
		int p=T;
		while(p!=S)
		{
			cap[lst[p]]-=flow[T];
			cap[(lst[p]&1)?lst[p]+1:lst[p]-1]+=flow[T];
			p=pre[p];
		}
	}
}
int main()
{
	m=read();n=read();S=1;T=m+n+2;
	for(int i=1;i<=m;i++)
	{
		int ai=read();
		add_e(S,i+1,0,ai);
		add_e(i+1,S,0,0);
	}
	for(int i=1;i<=n;i++)
	{
		int bi=read();
		add_e(i+m+1,T,0,bi);
		add_e(T,i+m+1,0,0);
	}
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=n;j++)
		{
			int cij=read();
			add_e(i+1,j+m+1,cij,inf);
			add_e(j+m+1,i+1,-cij,0);
		}
	}
	MinCostMaxFlow(1);
	printf("%d\n",ans);
	for(int i=2;i<=tot;i+=2){cap[i-1]+=cap[i];cap[i]=0;}
	ans=0;
	MinCostMaxFlow(-1);
	printf("%d\n",ans);
	return 0;
}