「USACO」Haywire

发表于 | 分类于 | | 浏览量： 次

什么神仙题目。蒟蒻我前前后后一共交了13次，才终于把这个退火搞懂了QwQ。

传送门

洛谷P2210

题解

蒟蒻我之前一直对模拟退火保持一个懵逼状态，今天是差不多把大概原理终于理清楚了QwQ。

其实基本上就是个退火的板子，但是蒟蒻我一直搞不清楚计算接受较差答案的概率。

一般来说，计算改成的式子是这样的：

exp((now-ans)/T)>rand()/RAND_MAX

其中now表示当前的答案，ans表示已知最优答案，也有可能是ans-now，总之应该是个负数。满足上式，则接受较差的答案。

其中$exp(x)$表示$e^x$，函数图像大概是这样的：

1.png

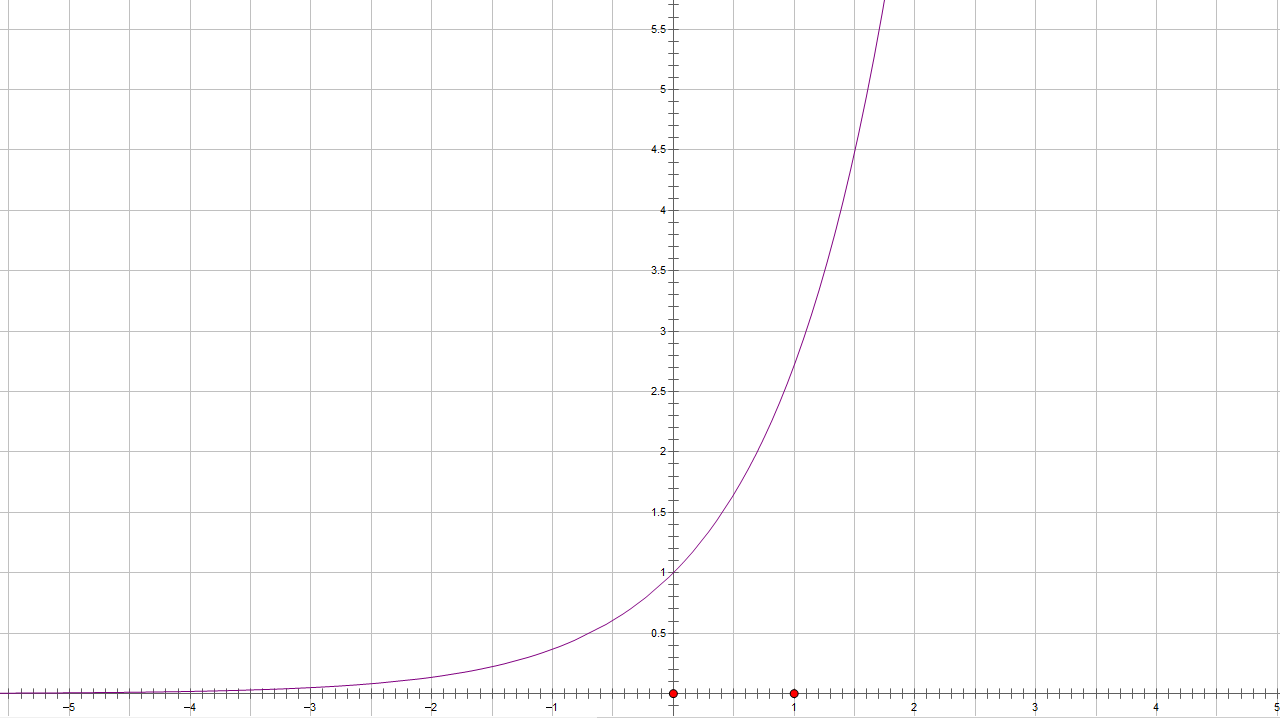
所以与当前最优答案差距越大，温度越低，$exp()$的值就越小，接受这个较差的答案的概率就越小。

还有，调参的时候，降温系数，停止退火的温度下限，温度初始值，退火的次数要一起调，尤其是退火的次数，多退几次还是很有必要的。种子可以用神仙学长ZZK的生日20020222。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
using namespace std;
const double delta=0.99;
int n,fri[20][5],Q[20],ans;
inline int Calc()
{
	int ret=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=3;j++)
			if(Q[i]>Q[fri[i][j]])
				ret+=Q[i]-Q[fri[i][j]];
	return ret;
}
inline void SA(double T)
{
	while(T>1e-12)
	{
		int a=rand()%n+1,b=rand()%n+1;
		while(a==b){a=rand()%n+1;b=rand()%n+1;}
		swap(Q[a],Q[b]);
		int now=Calc();
		if(now<ans) ans=now;
		else if(exp((ans-now)/T)<(double)rand()/RAND_MAX) swap(Q[a],Q[b]);
		T*=delta;
	}
}
int main()
{
	srand(19260817);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d%d%d",&fri[i][1],&fri[i][2],&fri[i][3]);
	for(int i=1;i<=n;i++) Q[i]=i;
	ans=Calc();
	for(int i=1;i<=500;i++) SA(19260817);
	printf("%d\n",ans);
	return 0;
}