「HNOI2016」树

发表于 | 分类于 | | 浏览量： 次

骚年，来看看这棵 真•树套树 吧！

传送门

洛谷

BZOJ

题解

蒟蒻我定睛一看，一共有$10^{10}$个点，立马把蒟蒻我给吓到了QwQ。显然这是一道毒瘤题。我深深地感受到了出题人的恶意(然而我还是太菜了，像XHW这种dalao就可以想着要把出题人阿掉，我却不行)。

既然有这么多点，肯定是存不下的。因为每次操作都是copy一整颗子树，所以我们可以用一种叫做 真•树套树 的方法来解决呢poi。

我们构造大树时，令每一个大节点都对应模板树中的一整棵子树，并对新树重新编号，就像这样（样例）：

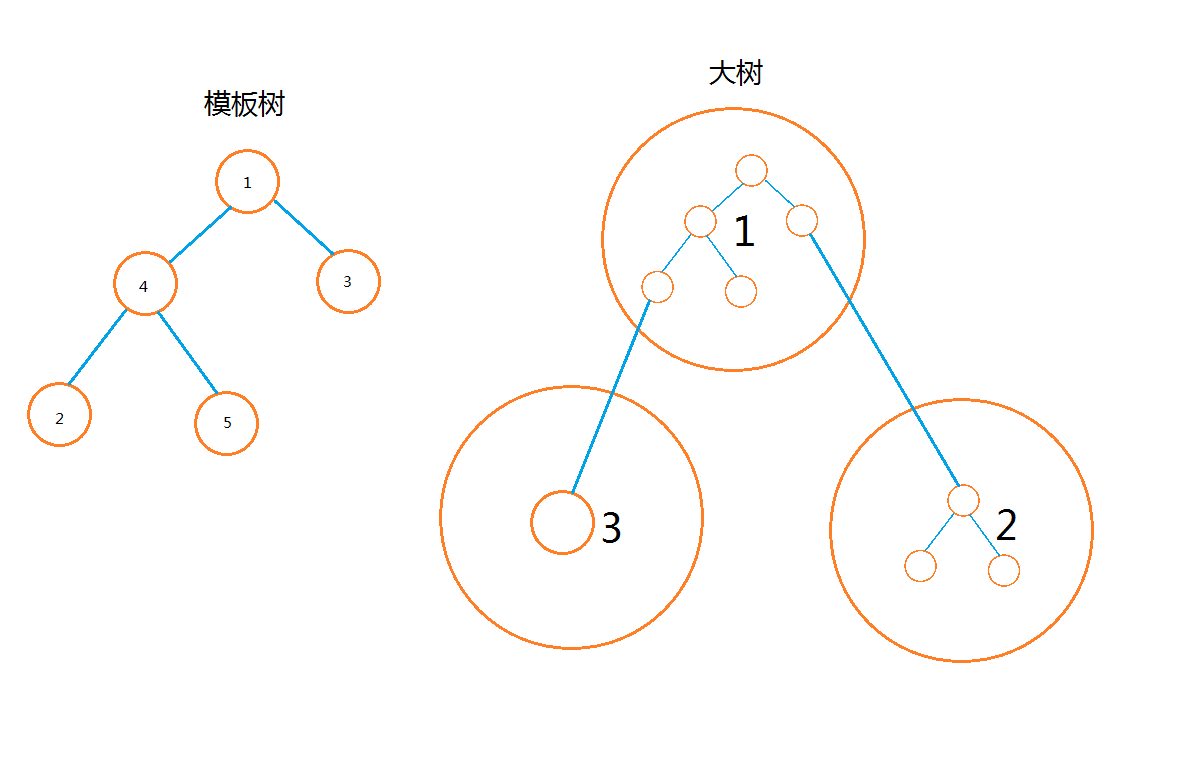
tree1

然后我们定义两个大节点之间的边的变权为两个大节点所包含的树的树根之间的距离。如上图中大节点1和2之间的边权为2,1与3之间的边权为3。

每一个大节点还需要存储以下信息：

  • S[],T[]：该大节点包含的小节点的编号区间的起点和终点，如上图节点1的编号区间是[1,5]，节点2是[6,8]，节点3是[9,9]。
  • pre[]：该大节点对应的是模板树中哪一个节点的子树，如pre[1]=1，pre[2]=4，pre[3]=3。
  • lnk[]：该大节点挂在大树中的哪一个节点底下，如lnk[2]=3，lnk[3]=2。

以及常见的倍增LCA所需的信息。

还需要写几个函数：

  • int GetRoot(long long u);用于查找小节点u所在的大节点。构造好S[],T[0]后，二分即可实现。
  • int GetPre(long long u);用于查找小节点u在模板树中对应的是哪个节点。假设小节点u在大节点rt里，那么根据题意，我们要找的就是rt对应的模板树的子树中该子树编号第$u-S[rt]+1$小的节点。这个我们可以把模板树一巴掌拍扁求个DFS序，然后用主席树解决（不会主席树的童鞋戳这里）。
  • int GetDist(int u,int v);用于求模板树上的节点u,v之间的距离。LCA解决。

然后就可以开始考虑如何计算答案了。

计算答案的主要思想就是在大树上通过倍增LCA求解，但是与普通LCA不同的是，不能纯粹地就在大树上LCA，需要注意很多细节。比如当再跳一步就跳到最近的大节点公共祖先时，不能马上往上跳，而需要往上跳一小步后转到模板树上去LCA。因为计算答案的细节，劳资%@#@￥%(文明靠大家)地交了4次才AC(不过好像也不算多)。

这样这题就解完了。时空复杂度都是大约$\Theta(超大常数*n\log n)$呢poi。

总结&反思

这是一道十分毒瘤的代码题(但是在某些dalao眼里就是送分题)，思维难度一般，但蒟蒻我前前后后一共花了3个多小时才AC(听说隔壁XCW一看题就秒掉了)QwQ。这道题很好地反映出蒟蒻我的代码实现能力还是太差，可能是由于做题太少的缘故。我虽然很菜，但是如果ZJOI2019真的出了像这样的一道题(或者类似于猪国杀什么的)，空有想法却没时间写代码和调试，那可就亏大发了QwQ。

代码

蒟蒻我为了避免变量重名，于是开了两个namespace（不知代码是更好看了还是更丑了）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
const int maxn=100005,LOG=20;
int Q;
inline LL read()
{
	LL ret=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-f;ch=getchar();}
	while(ch>='0'&&ch<='9'){ret=ret*10+ch-'0';ch=getchar();}
	return ret*f;
}
struct ChairmanTree               //封装好的主席树
{
	int tot,T[maxn];
	struct Node{int L,R,Sum;}Tree[maxn*LOG];
	int Build(int L,int R)
	{
		int rt=++tot,mid=L+R>>1;
		if(L>=R) return rt;
		Tree[rt].L=Build(L,mid);
		Tree[rt].R=Build(mid+1,R);
		if(rt==1) T[0]=rt;
		return rt;
	}
	int Update(int num,int pre,int L,int R)
	{
		int rt=++tot,mid=L+R>>1;
		Tree[rt].L=Tree[pre].L;Tree[rt].R=Tree[pre].R;Tree[rt].Sum=Tree[pre].Sum+1;
		if(L>=R) return rt;
		if(num<=mid) Tree[rt].L=Update(num,Tree[pre].L,L,mid);
		else Tree[rt].R=Update(num,Tree[pre].R,mid+1,R);
		return rt;
	}
	int Query(int u,int v,int k,int L,int R)
	{
		int mid=L+R>>1,x=Tree[Tree[v].L].Sum-Tree[Tree[u].L].Sum;
		if(L==R) return mid;
		if(x>=k) return Query(Tree[u].L,Tree[v].L,k,L,mid);
		else return Query(Tree[u].R,Tree[v].R,k-x,mid+1,R);
	}
}CT;
namespace TemplateTree           //模板树
{
	int n,father[maxn][LOG],dep[maxn],idx,que[maxn],S[maxn],T[maxn],tot,lnk[maxn],son[maxn*2],nxt[maxn*2];
	inline void add_e(int x,int y){tot++;son[tot]=y;nxt[tot]=lnk[x];lnk[x]=tot;}
	void Build(int now,int fa)   //把树上的一些信息构造好
	{
		S[now]=++idx;que[idx]=now;father[now][0]=fa;dep[now]=dep[fa]+1;
		for(int i=1;i<=16;i++) father[now][i]=father[father[now][i-1]][i-1];
		for(int i=lnk[now];i;i=nxt[i])
			if(son[i]!=fa)
				Build(son[i],now);
		T[now]=idx;
	}
	inline void BuildCT()      //初始化主席树
	{
		CT.Build(1,n);
		for(int i=1;i<=n;i++) CT.T[i]=CT.Update(que[i],CT.T[i-1],1,n);
	}
	inline void Input()       //读入数据
	{
		for(int i=1;i<n;i++)
		{
			int a=read(),b=read();
			add_e(a,b);add_e(b,a);
		}
		Build(1,0);BuildCT();
	}
	int GetDist(int u,int v)    //LCA求亮点间距离
	{
		int ret=0;
		if(dep[u]<dep[v]) swap(u,v);
		for(int i=16;i>=0;i--) if(dep[father[u][i]]>=dep[v]){ret+=(1<<i);u=father[u][i];}
		for(int i=16;i>=0;i--) if(father[u][i]!=father[v][i]){ret+=(1<<i+1);u=father[u][i];v=father[v][i];}
		if(u==v) return ret;
		return ret+2;
	}
}
namespace BigTree             //大树
{
	int n,m,father[maxn][LOG],dep[maxn],pre[maxn];LL dist[maxn][LOG],S[maxn],T[maxn],lnk[maxn],cnt;
	inline int GetRoot(LL u)
	{
		int L=1,R=n,mid;
		while(L<=R)
		{
			mid=L+R>>1;
			S[mid]<=u?L=mid+1:R=mid-1;
		}
		return R;
	}
	inline int GetPre(LL u)
	{
		int rt=GetRoot(u);
		return CT.Query(CT.T[TemplateTree::S[pre[rt]]-1],CT.T[TemplateTree::T[pre[rt]]],u-S[rt]+1,1,TemplateTree::n);
	}
	inline void Build()        //初始化大树
	{
		n=1;dep[1]=1;pre[1]=1;S[1]=1;T[1]=TemplateTree::n;cnt=T[1];
		for(int i=1;i<=m;i++)
		{
			int fr=read();LL to=read();int rt=GetRoot(to);
			n++;dep[n]=dep[rt]+1;lnk[n]=to;pre[n]=fr;S[n]=cnt+1;T[n]=cnt+TemplateTree::T[fr]-TemplateTree::S[fr]+1;cnt=T[n];
			father[n][0]=rt;dist[n][0]=TemplateTree::dep[GetPre(to)]-TemplateTree::dep[pre[rt]]+1;
			for(int j=1;j<=16;j++){father[n][j]=father[father[n][j-1]][j-1];dist[n][j]=dist[n][j-1]+dist[father[n][j-1]][j-1];}
		}
	}
	inline LL Solve(LL u,LL v)     //计算答案(写的真丑QwQ)
	{
		LL ret=0;int rtu=GetRoot(u),rtv=GetRoot(v);
		if(rtu==rtv) return TemplateTree::GetDist(GetPre(u),GetPre(v));
		if(dep[rtu]<dep[rtv]){swap(u,v);swap(rtu,rtv);}
		ret+=TemplateTree::dep[GetPre(u)]-TemplateTree::dep[pre[rtu]];u=rtu;
		for(int i=16;i>=0;i--) if(dep[father[u][i]]>dep[rtv]){ret+=dist[u][i];u=father[u][i];}
		if(GetRoot(lnk[u])==rtv) return ret+1+TemplateTree::GetDist(GetPre(lnk[u]),GetPre(v));
		ret+=TemplateTree::dep[GetPre(v)]-TemplateTree::dep[pre[rtv]];v=rtv;
		if(dep[u]>dep[v]){ret+=dist[u][0];u=father[u][0];}
		for(int i=16;i>=0;i--) if(father[u][i]!=father[v][i]){ret+=dist[u][i]+dist[v][i];u=father[u][i];v=father[v][i];}
		u=lnk[u];v=lnk[v];ret+=2;
		return ret+TemplateTree::GetDist(GetPre(u),GetPre(v));
	}
}
int main()                    //好简洁的主函数
{
	TemplateTree::n=read();BigTree::m=read();Q=read();
	TemplateTree::Input();BigTree::Build();
	while(Q--) printf("%lld\n",BigTree::Solve(read(),read()));
	return 0;
}